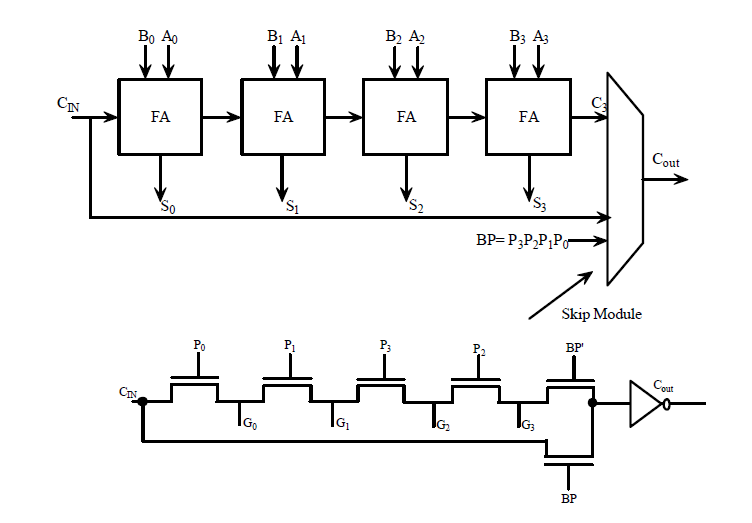
Carry-save Adder Crack + Download Carry-save adder is designed to add two numbers using the carry-save method, in which each adder carries its bit to the next adder, which is then added to the current partial carry results, one at a time. This addition process continues until all of the numbers have been added. Carry-save adder is a parallel adder. The general structure of this design is: The input of the carry-save adder is: Input A Input B Output 4 stages with one-bit adders 4 stages with one-bit adders 6 stages with two-bit adders 6 stages with two-bit adders Stage 1 Stage 2 Stage 3 Stage 4 Stage 5 Stage 6 In the first stage of the carry-save adder, the first pair of input A and B are added in the one-bit adder. The output of the first stage is the carry out bit of the first adder. The output of the second stage is the carry out bit of the second adder. The second stage is similar to the first stage. The output of the first stage is the carry out bit of the first adder. The output of the second stage is the carry out bit of the second adder. In the third stage, two bits of the first carry bit of the first adder and carry bit of the second adder are added in the two-bit adder. The output of the third stage is the carry out bit of the third adder. The fourth stage is similar to the third stage. The output of the fourth stage is the carry out bit of the third adder. In the fifth stage, the addition of the result from the second stage and the third stage is performed in the two-bit adder. The result of the addition is the sum of A and B. The output of the fifth stage is the carry out bit of the fifth adder. In the sixth stage, the sum of the fifth result and the carry out bit from the fourth stage is added in the two-bit adder. The output of the sixth stage is the carry out bit of the sixth adder. The operation of the carry-save adder is shown below: How to Make a Carry-Save Adder Step by Step: There are many ways to do Carry-save Adder Crack+ [Mac/Win] Outputs: End of this chapter: .. index:: single: Carry-save Adder The carry-save adder ==================== The carry-save adder is designed to offer you a simplified graphical representation of the circuit, which includes one-bit adders. The following figure shows a carry-save adder circuit, where the carry out is connected to the negative output. It also shows the input and output bits connected to the register, the numbers on the input, output and carry lines represent the number of input, output and carry bits, respectively. .. figure:: /_images/CASA-circuit.png :alt: Carry-save adder circuit :align: center Carry-save adder circuit .. code-block:: verilog :class:`. module CASA(input [7:0] [8:0] add_in, input clk, output reg carry_out, input [6:0] [7:0] input_in, output reg [7:0] output_in); // Carry-save adder inputs wire [7:0] add_out = add_in; wire [7:0] res_out; wire carry_out = ~carry_out; wire [6:0] carry_in; wire [7:0] res_in; // Carry-save adder outputs reg [7:0] product; reg [7:0] partial; // Carry-in inputs wire [3:0] carry_in1 = carry_in[4:2]; wire [3:0] carry_in2 = carry_in[1:0]; 1a423ce670 Carry-save Adder PC/Windows ADDENDUM key The first three digits of the algorithm are the name of the author or the producer of the algorithm. The following 14 letters or numbers are the algorithm. Carry-save adder, or Carry-save adder with summation, or carry-save adder with summation, or Carry-save adder with summation, or Carry-save adder with summation. Carry-save adder is a simple adder, which deals with a sum of addition. It is a carry-save adder with summation. Carry-save adder is a type of adder with summation. In the figure, it shows a simple carry-save adder. Carry-save adder without summation is an adder with summation. In the figure, it shows a simple carry-save adder without summation. A: Not sure how it is used, but I suspect that Carry-Save Adder is used in methods like this: private static int addWithAdderAndCarry(int a, int b) { int c = a + b; int d = c >>> 16; int e = c & 0xFFFF; int f = d + e; return f; } Because the Carry-Save Adder is typically simpler to implement than the Full Adder, this is a method used by many languages to implement addition. Of course, it could be used in other ways, e.g., it could be used to implement an associative language. And actually, when I look at the Java Language Specification (JLS), it does mention Carry-Save Adders in the Introduction. What's New in the Carry-save Adder? System Requirements: Gamers who have just bought The Walking Dead's PS3 or 360 edition and are interested in extending their experience can download this Special Edition for free. Just log in to your participating account on the PlayStation Network or Xbox Live Marketplace and you will find it under "Redeem Codes". This is the Extended Edition of the game that includes all episodes from Seasons 1 and 2 of the television series, the game's original story campaign "400 Days" and the additional story campaign "The Hundred". Buy The Walking Dead - Season 2 Bundle Edition on the PlayStation Store today! Game
Related links:
Comments